How to calculate the algebraic expansion of the powers of a binomial

The formulas for calculating the most frequent powers of the binomial (a + b)

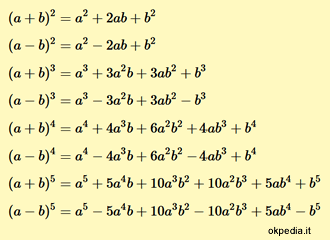
Exercises and examples

Exercise 1

$$ (x+2)^2 $$

$$ x^2 + 2 \cdot 2x + 2^2 $$

$$ x^2 + 4x + 4 $$

Exercise 2

$$ (x-2)^3 $$

$$ x^3 - 3 \cdot 2x^2 + 3 \cdot 2^2x - 2^3 $$

$$ x^3 - 6x^2 + 12x - 8 $$

How to calculate the nth power of the binomial

To calculate the nth power of a binomial

$$ (a+b)^n $$

Write a homogeneous polynomial using the first variabile. The power must be decreasing from 0 to n.

$$ a^n+a^{n-1}+...+a^1+1 $$

Write a polynomial using the second variable. The power must be increasing from 0 to n.

$$ 1+b^1+b^2+...+b^{n-1}+...+b^n $$

Multiply the two polynomials

$$ a^n+a^{n-1}b^1+...+a^1b{n-1}+b^n $$

Write the coefficients to the polynomial using Tartaglia's triangle.

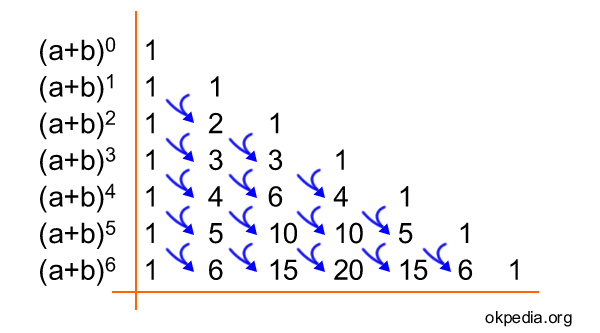
Each number in the triangle is equal to the sum of the two numbers on the top and top left.

Note. If the sign of the binomial is minus, alternate plus and minus in the polynomial.

Examples

Example 1 (square of the binomial)

Calculate the square of the binomial:

$$ (a+b)^2 $$

$$ a^2 + 2ab + b^2 $$

Example 2 (binomial cube)

Calculate the cube of the binomial:

$$ (a+b)^3 $$

$$ a^3 + 3a^2b + 3ab^2 + b^3 $$

Example 3

Calculate the following binomial:

$$ (a+b)^4 $$

$$ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$

The formulas of the power of the binomial

$$ (a+b)^2 = a^2+2ab+b^2 $$ $$ (a-b)^2 = a^2-2ab+b^2 $$ $$ (a+b)^3 = a^3+3a^2b+3ab^2+b^3 $$ $$ (a-b)^3 = a^3-3a^2b+3ab^2-b^3 $$ $$ (a+b)^4 = a^4+4a^3b+6a^2b^2+3ab^3+b^4 $$ $$ (a-b)^4 = a^4-4a^3b+6a^2b^2-3ab^3+b^4 $$ $$ (a+b)^5 = a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5 $$ $$ (a-b)^5 = a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5 $$