Calcular la potencia de un binomio

Las fórmulas para calcular las potencias más frecuentes de un binomio (a + b)

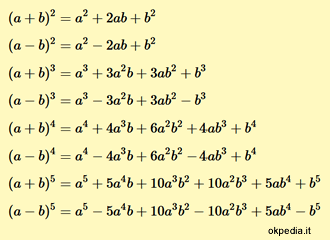
Ejercicios y ejemplos

Ejercicio 1

$$ (x+2)^2 $$

$$ x^2 + 2 \cdot 2x + 2^2 $$

$$ x^2 + 4x + 4 $$

Ejercicio 2

$$ (x-2)^3 $$

$$ x^3 - 3 \cdot 2x^2 + 3 \cdot 2^2x - 2^3 $$

$$ x^3 - 6x^2 + 12x - 8 $$

Cómo calcular la fórmula de la potencia n-ésima de un binomio

Para calcular la n-ésima potencia de un binomio

$$ (a+b)^n $$

Escribe un polinomio homogéneo, de grado igual al binomio, usando una potencia decreciente de la primera variable de n a 0.

$$ a^n+a^{n-1}+...+a^1+1 $$

Escribe un polinomio con potencia creciente de la segunda variable de 0 a n.

$$ 1+b^1+b^2+...+b^{n-1}+...+b^n $$

Multiplica los términos respectivos de los dos polinomios.

$$ a^n+a^{n-1}b^1+...+a^1b{n-1}+b^n $$

Escribe los coeficientes del polinomio a través del triángulo de Tartaglia.

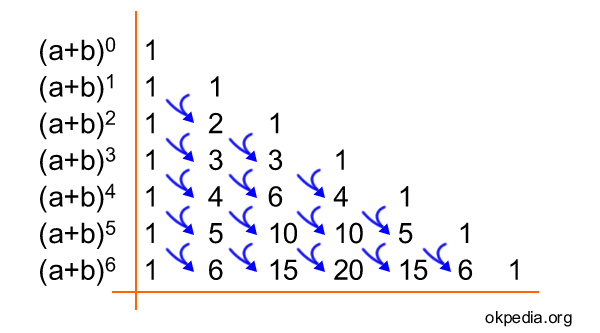
Cada número en el triángulo es igual a la suma de los dos números arriba y arriba a la izquierda.

Nota. Si el signo del binomio es menos, alterna más y menos en el polinomio.

Ejemplos

Ejemplo 1 (cuadrado de un binomio)

Calcular el cuadrado de un binomio:

$$ (a+b)^2 $$

$$ a^2 + 2ab + b^2 $$

Ejemplo 2 (cubo binomial)

Calcular el cubo de un binomio:

$$ (a+b)^3 $$

$$ a^3 + 3a^2b + 3ab^2 + b^3 $$

Ejemplo 3

Calcula el siguiente binomio:

$$ (a+b)^4 $$

$$ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$

Las fórmulas de la potencia de un binomio

$$ (a+b)^2 = a^2+2ab+b^2 $$ $$ (a-b)^2 = a^2-2ab+b^2 $$ $$ (a+b)^3 = a^3+3a^2b+3ab^2+b^3 $$ $$ (a-b)^3 = a^3-3a^2b+3ab^2-b^3 $$ $$ (a+b)^4 = a^4+4a^3b+6a^2b^2+3ab^3+b^4 $$ $$ (a-b)^4 = a^4-4a^3b+6a^2b^2-3ab^3+b^4 $$ $$ (a+b)^5 = a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5 $$ $$ (a-b)^5 = a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5 $$