Calcolare la potenza del binomio

Le formule per calcolare le più frequenti potenze del binomio (a+b)

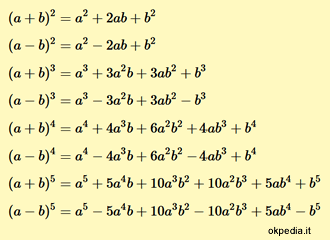
Esercizi ed esempi

Esercizio 1

$$ (x+2)^2 $$

$$ x^2 + 2 \cdot 2x + 2^2 $$

$$ x^2 + 4x + 4 $$

Esercizio 2

$$ (x-2)^3 $$

$$ x^3 - 3 \cdot 2x^2 + 3 \cdot 2^2x - 2^3 $$

$$ x^3 - 6x^2 + 12x - 8 $$

Come calcolare la formula della potenza ennesima del binomio

Per calcolare la potenza ennesima di un binomio

$$ (a+b)^n $$

Scrivere un polinomio omogeneo, di grado uguale al binomio, con potenza decrescente della prima variabile da n a 0.

$$ a^n+a^{n-1}+...+a^1+1 $$

Scrivere un polinomio con potenza crescente della seconda variabile da 0 a n.

$$ 1+b^1+b^2+...+b^{n-1}+...+b^n $$

Moltiplicare i rispettivi termini dei due polinomi

$$ a^n+a^{n-1}b^1+...+a^1b{n-1}+b^n $$

Aggiungere i coefficienti al polinomio tramite il triangolo di Tartaglia.

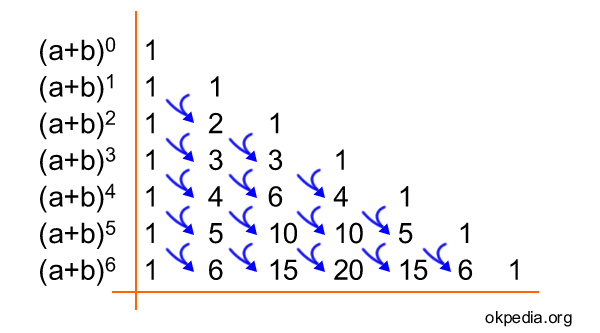
Ogni numero del triangolo è uguale alla somma dei due numeri in alto e in alto a sinistra.

Nota. Se il segno del binomio è meno alternare più e meno nel polinomio.

Esempi

Esempio 1 ( quadrato del binomio )

Calcolare il quadrato del binomio:

$$ (a+b)^2 $$

$$ a^2 + 2ab + b^2 $$

Esempio 2 ( cubo del binomio )

Calcolare il cubo del binomio:

$$ (a+b)^3 $$

$$ a^3 + 3a^2b + 3ab^2 + b^3 $$

Esempio 3

Calcolare il seguente binomio:

$$ (a+b)^4 $$

$$ a^4 + 4a^3b + 6a^2b^2 + 4ab^3 + b^4 $$

Le formule della potenza del binomio

$$ (a+b)^2 = a^2+2ab+b^2 $$ $$ (a-b)^2 = a^2-2ab+b^2 $$ $$ (a+b)^3 = a^3+3a^2b+3ab^2+b^3 $$ $$ (a-b)^3 = a^3-3a^2b+3ab^2-b^3 $$ $$ (a+b)^4 = a^4+4a^3b+6a^2b^2+3ab^3+b^4 $$ $$ (a-b)^4 = a^4-4a^3b+6a^2b^2-3ab^3+b^4 $$ $$ (a+b)^5 = a^5+5a^4b+10a^3b^2+10a^2b^3+5ab^4+b^5 $$ $$ (a-b)^5 = a^5-5a^4b+10a^3b^2-10a^2b^3+5ab^4-b^5 $$