Come trovare la retta normale
Per calcolare l'equazione della retta perpendicolare in un punto della funzione f(x), detta retta normale, si applica la seguente formula:
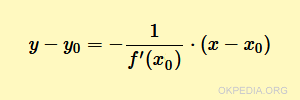
- Le variabili x0,y0 sono le coordinate (x0,y0) del punto P della funzione.
- La funzione f'(x0) è il valore della la derivata prima della funzione f(x) con x=x0.
La formula determina l'equazione cartesiana della retta normale ad eccezione del caso in cui f'(x0)=0 ( retta orizzontale ).
Cos'è la retta normale? La retta normale ( normal line ) è una retta perpendicolare alla retta tangente ( tangent line ) in un punto P(x,y) della funzione y=f(x). La retta normale e la retta tangente formano quattro angoli di 90°.
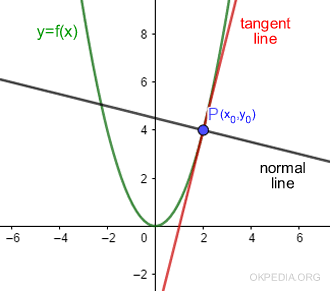
Esempio di calcolo
Data una funzione f(x)=x2 trovare la retta tangente nel punto P(2,4).
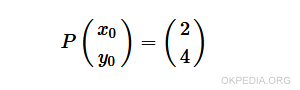
L'equazione della retta normale si calcola usando la seguente formula con x0=2 e y0=4
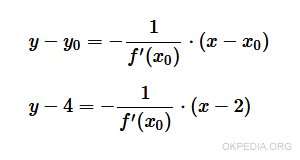
Nota. La derivata prima della funzione f'(x) in x0=2 è uguale a 4.
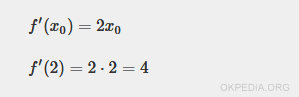
Il coefficiente angolare della retta perpendicolare al punto P è -1/4.
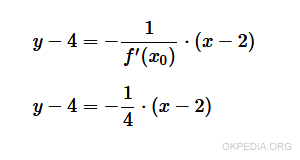
L'equazione in forma esplicita della retta normale è
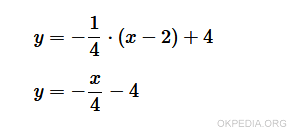
E' l'equazione della retta perpendicolare alla retta tangente della funzione nel punto P.
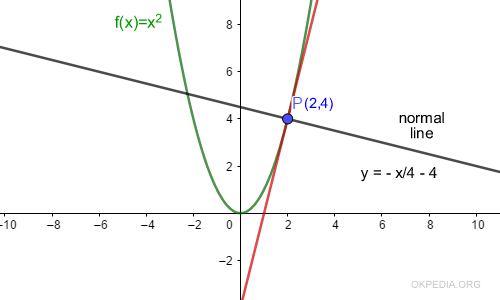
Attenzione. La formula per calcolare la retta normale non è applicabile se f'(x0)=0 ossia se la retta normale è orizzontale e parallela all'asse delle ascisse. In tale punto la retta perpendicolare potrebbe esistere oppure no, la formula non riesce a calcolare l'equazione cartesiana della retta perché il rapporto -1/f'(x0) diventa infinito.
