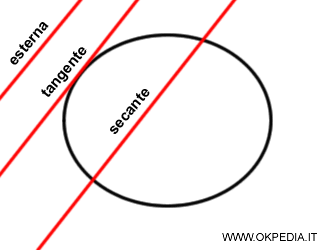
Come capire se una retta è esterna, secante o tangente

Per verificare se una retta è esterna, secante o tangente a una funzione, si calcola il sistema di equazioni composto dall'equazione della retta e dalla funzione.

• Se il sistema ha una soluzione, la retta è tangente.
• Se il sistema ha due equazioni, la retta è secante.
• Se il sistema non ha soluzioni, la retta è esterna.

Esempio

Data una retta

$$ x-y=1 $$

e una circonferenza

$$ (x-2)^2 + (y-2)^2 = 1 $$

Per verificare se la retta è tangente alla circonferenza si calcola il sistema di equazioni:

$$ \begin{cases} x-y=1 \\ (x-2)^2 + (y-2)^2 = 1 \end{cases} $$

Si trovano le eventuali soluzioni del sistema

$$ \begin{cases} x=y+1 \\ (x-2)^2 + (y-2)^2 = 1 \end{cases} $$

$$ \begin{cases} x=y+1 \\ ((y+1)-2)^2 + (y-2)^2 = 1 \end{cases} $$

$$ \begin{cases} x=y+1 \\ (y-1)^2 + (y-2)^2 = 1 \end{cases} $$

$$ \begin{cases} x=y+1 \\ y^2-2y+1 + y^2-4y+4 = 1 \end{cases} $$

$$ \begin{cases} x=y+1 \\ 2y^2-6y+4 = 0 \end{cases} $$

$$ \begin{cases} x=y+1 \\ y^2-3y+2 = 0 \end{cases} $$

L'equazione ha due soluzioni

$$ y^2-3y+2 = 0 $$

$$ y= \frac{-b \pm \sqrt{b^2-4ac} }{2a} $$

$$ y= \frac{3 \pm \sqrt{3^2 - 4 \cdot 1 \cdot 2} }{2 \cdot 1} $$

$$ y= \frac{3 \pm \sqrt{9 - 8 } } {2 \cdot 2} $$

$$ y= \frac{3 \pm 1}{2} = \begin{cases} y_1=2 \\ y_2=1 \end{cases}$$

Il sistema ha due soluzioni.

Soluzione 1

$$ \begin{cases} x=y+1 = 3 \\ y_1 = 2 \end{cases} $$

Soluzione 2

$$ \begin{cases} x=y+1 = 2 \\ y_2 = 1 \end{cases} $$

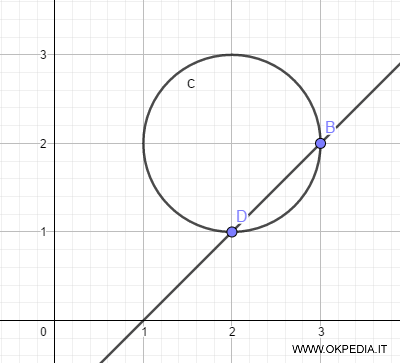
Pertanto, la retta è secante alla ciconferenza alle coordinate (x,y)=(3,2) e (x,y)=(2,1).