Trovare retta tangente a un grafico e parallela a una retta

Per calcolare la retta tangente al grafico di una funzione f(x) e parallela a una retta

1. Data la retta ax+by+cy calcolare il coefficiente angolare della retta $$ m = - \frac{a}{b} $$
2. Calcolare la derivata prima della funzione f(x) $$ f'(x) $$ La derivata prima della funzione in un punto qualsiasi x₀ è uguale il coefficiente angolare della funzione nel punto x₀.
3. Risolvere il sistema per x e trovare il valore x₀ in cui i coefficienti angolari si eguagliano. $$ f'(x) = - \frac{a}{b} $$
4. Calcolare il valore della funzione y=f(x) in x₀ per trovare le coordinate (x₀,y₀) del punto di tangenza. $$ y_0 = f(x_0) $$
5. Trovare l'equazione della retta tangente nel punto P (x₀,y₀) $$ y - y_0 = m ( x - x_0 ) $$

Esempio

Data una funzione e una retta

$$ f(x) = x^2 $$

$$ y - x - 1 = 0 $$

La rappresentazione grafica

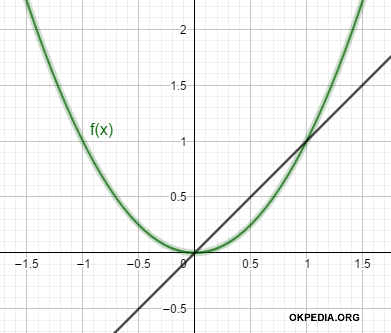
I coefficienti angolari della funzione e della retta sono

$$ f'(x) = 2x $$

$$ m = -\frac{-1}{1} = 1 $$

Trovare il valore di x che eguaglia i due coefficienti angolari

$$ f'(x) = m $$

$$ 2x = 1 $$

$$ x = \frac{1}{2} $$

Trovare il valore corrispondente della y

$$ y = f ( x ) = x^2 = ( \frac{1}{2} )^2 = \frac{1}{4} $$

Il punto di tangenza è

$$ P = \begin{pmatrix} x_0 \\ y_0 \end{pmatrix} = \begin{pmatrix} \frac{1}{2} \\ \frac{1}{4} \end{pmatrix} $$

Calcolare la retta dell'equazione tangente

$$ y - y_0 = m \cdot ( x - x_0 ) $$

$$ y - \frac{1}{4} = 1 \cdot ( x - \frac{1}{2} ) $$

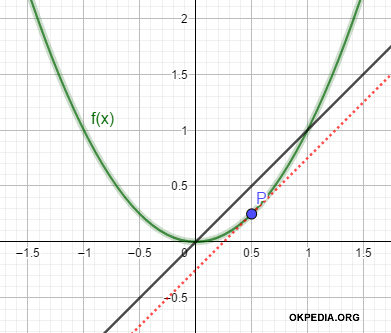
$$ y = x - \frac{1}{4} $$

La rappresentazione grafica