Calcolare integrale indefinito con python
Per trovare la funzione primitiva ( integrale indefinito o antiderivata ) di una funzione matematica f(x) in python, si usa la funzione integrate della libreria sympy.
integrate(f,x)
- Il primo argomento f è la funzione integranda da integrare
- Il secondo argomento x è la variabile di integrazione (dx). La variabile deve essere definita come simbolo.
La funzione integrate() restituisce in output la funzione primitiva F(x).
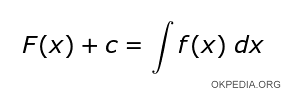
Nota. La funzione integrate() effettua l'integrazione indefinita di una funzione, ossia l'operazione inversa della derivazione. A partire da una funzione derivata f'(x) in input calcola la funzione primitiva f(x) in output. Per questa ragione l'operazione di integrazione indefinita è anche detta antiderivata.
Esempi di calcolo
Esempio 1
Questo script calcola l'integrale indefinito della funzione 2x.
import sympy as sp
x = sp.Symbol('x')
sp.integrate(2*x, x)
La prima istruzione carica la libreria sympy in memoria.
La seconda istruzione definisce la variabile x come un simbolo tramite la funzione Symbol().
La terza istruzione calcola l'integrale della funzione 2*x tramite integrate().
Il risultato in output è il seguente
x**2
La funzione primitiva di 2x è x2.
$$ \int 2x \; dx = x^2 +c $$
Esempio 2
Questo script calcola la funzione primitiva di sin(x)
import sympy as sp
y=sp.sin(x)
sp.integrate(y, x)
La funzione ritorna in output il risultato
-cos(x)
La funzione primitiva di sin(x) è -cos(x).
$$ \int sin x \; dx = -cos x +c $$
Esempio 3
Questo script calcola l'integrale indefinito di x/5
import sympy as sp
y=x/5
sp.integrate(y, x)
Il risultato dello script è il seguente:
x**2/10
La funzione primitiva di x/5 è x2/10.
$$ \int \frac{x}{5} \; dx = \frac{x^2}{10} +c $$
