Come calcolare la matrice inversa
Per trovare la matrice inversa M-1 di una matrice quadrata M si usa la seguente formula.
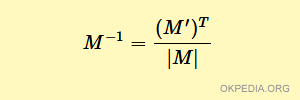
Esempio
- Data una matrice quadrata M
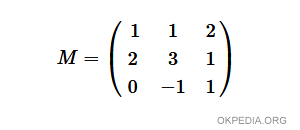
- Calcolare il determinante della matrice M
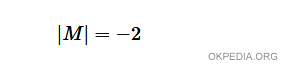
- Se il determinante è diverso da zero, la matrice M è una matrice invertibile.
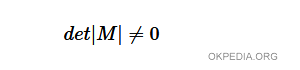
Nota. Se il determinante è uguale a 0, la matrice M non è invertibile e non esiste la matrice inversa. In questo caso il procedimento termina qui.
- Calcolare la matrice dei cofattori M' o matrice dei complementi algebrici.
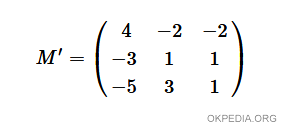
- Trovare la matrice trasposta della matrice dei cofattori (M')T.
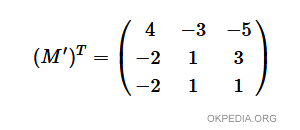
- Dividere la matrice trasposta (M')T per il determinante |M|.
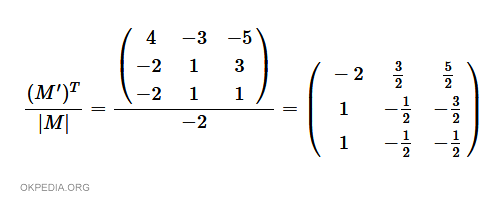
- Il risultato è la matrice inversa M-1.
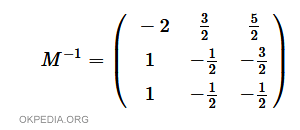
Verifica. Per verificare se la matrice M-1 è l'inversa di M, moltiplicare le due matrici tra loro. Il prodotto M-1 M è sempre una matrice identità.
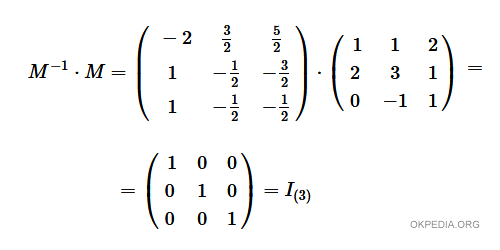
https://how.okpedia.org/it/matematica/come-calcolare-la-matrice-inversa
Hai una domanda? Scrivila nei commenti e ti risponderemo qui sulla pagina.
