Cos'è il rapporto incrementale

Il rapporto incrementale è la variazione media tra due punti x e x+Δx di una funzione continua f(x). Dove Δx è l'incremento. $$ \frac{f(x+Δx)-f(x)}{Δx} $$

E' anche detto tasso medio di variazione o di accrescimento.

In una funzione il rapporto incrementale è il rapporto tra Δy e Δx

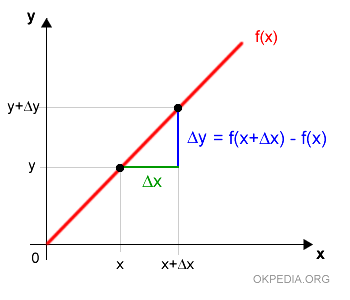
Nota. Il rapporto incrementale può comunque misurare anche la variazione media tra due punti qualsiasi (a,b) della funzione. $$ \frac{Δy}{Δx} = \frac{f(b)-f(a)}{b-a} $$

Un esempio pratico

Data una funzione continua nell'insieme dei numeri reali R

$$ f(x)=2x $$

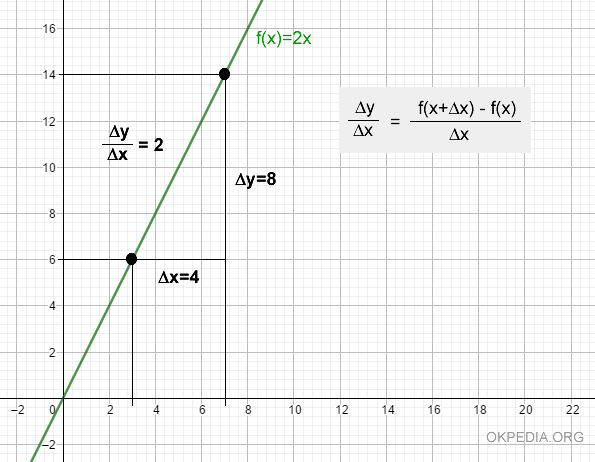
Prendiamo come riferimento il punto x=3 e un incremento Δx=4

$$ x=3 \\ Δx=4 $$

I valori della funzione nel punto x e x+Δx sono

$$ f(x)=f(3)=2(3)=6 \\ f(x+Δx)=f(3+4)=f(7)=2(7)=14 $$

Il rapporto incrementale è

$$ \frac{f(x+Δx)-f(x)}{Δx}= \frac{14-6}{4} = \frac{8}{4} = 2 $$

Questo vuol dire che per ogni incremento unitario Δx=1 la funzione y incrementa di Δy=2.

$$ \frac{Δy}{Δx} = \frac{2}{1} = 2 $$

La rappresentazione del rapporto incrementale sul diagramma cartesiano

Nota. Il limite del rapporto incrementale per Δx tendente a zero consente di calcolare la derivata di una funzione nel punto x.