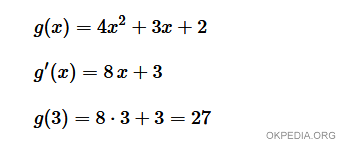Calculating the Derivative at a Specific Point Using Python

To compute the derivative of a mathematical function f(x) at a specific point using Python, one can utilize the `derivative()` function from the `misc` module of `scipy`.

from scipy import misc
def f(x):
...
misc.derivative(f,x0)

• The first argument, `f`, represents the function for which the derivative is to be calculated.
• The second argument, `x<sub>0</sub>`, denotes the point at which the derivative is evaluated.

The derivative() function determines the first derivative of f(x) at the specified point x₀.

So, what exactly is the derivative at a point? It represents the value of the derivative f '(x) when x = x₀.

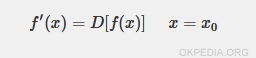
Examples

Example 1

Consider the function f(x)=x²

$$ f(x) = x^2 $$

To determine the derivative of f(x) at the point x = 4:

>>> from scipy import misc
>>> def f(x):
return x*x
>>> misc.derivative(f,4)

The derivative() function computes the value of the first derivative f'(x) at x = 4.

The resulting value is 8.0, implying that the first derivative of f(x) at x = 4 is 8.

8.0

Verification:

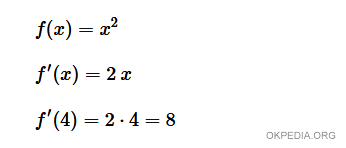
Example 2

For this example, we'll define a slightly more intricate function g(x) = 4x² + 3x + 2.

$$ g(x) = 4x^2 + 3x + 2 $$

To compute the derivative of g(x) at x = 3:

>>> from scipy import misc
>>> def g(x):
return 4*x**2+3*x+2
>>> misc.derivative(g,3)

The computed value is 27.0, signifying that the first derivative of g(x) at x = 3 is 27.

27.0

Verification