How to calculate derivative in python

To calculate the first, second or third derivative with the python language, we use the diff () function of the sympy library

diff(y,x)

or alternatively

y.diff(x)

The diff () function has at least two parameters

• The first argument y is the function to derive.
• The second argument x is the derivative variable.

The function diff() returns the derivative of the function as output.

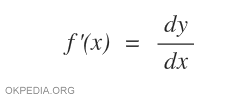
Note. It is a function of the sympy module. Therefore, by function you need to install and import the sympy library on Python. Furthermore, it is necessary to define the variable x as a symbol.

Calculation example

Example 1 (first derivative)

This script calculates the derivative of f(x)= x²+1

import sympy as sp
x = sp.Symbol('x')
y = x**2 + 1
sp.diff(y,x)

The result is

2*x

The first derivative of x²+1 is 2x.

Example 2 (first derivative)

This script calculates the first derivative of f(x)= x³

import sympy as sp
x = sp.Symbol('x')
y = x**3
y.diff(x)

The result of the operation is as follows

3*x**2

The first derivative of x³ is 3x².

Example 3 (second derivative)

This script calculates the second derivative of the function f(x)=x²

import sympy as sp
x = sp.Symbol('x')
y = x**2
sp.diff(y,x,x)

In this case the derivative variable (x) is indicated twice in a row.

Alternatively, the value 2 can also be indicated as the third parameter.

The output result is as follows

2

The second derivative of x² is 2

The first derivative of x² is 2x and the first derivative of 2x is 2. Therefore the second derivative of x² is 2.

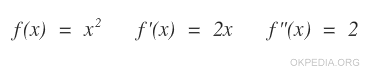
By adding the derivative variable other times, you can also calculate the third, fourth or fifth derivative of the function.

Alternatively, the degree of derivation can be indicated as the third parameter.

Example 3 (third derivative)

This script calculates the third derivative of the function f(x)=x²

import sympy as sp
x = sp.Symbol('x')
y = x**2
sp.diff(y,x,3)

The result is as follows

0

The third derivative of x² is zero.