How to calculate arctangent in Python

To calculate the arctangent (arctan) in Python, you can use the arctan() function from the NumPy module.

arctan(x)

The parameter x represents the tangent of an angle θ measured in radians.

The function outputs the arctangent.

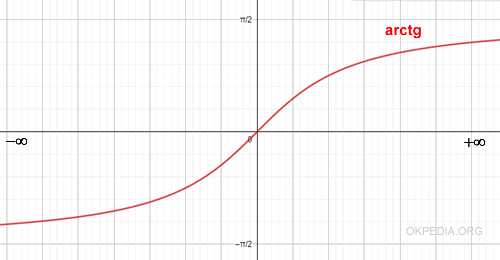
Arctangent is the inverse trigonometric function of tangent, denoted as arctan = tan^-1. It takes values between -π/2 and +π/2 radians in trigonometry.

Method 2 ( atan2 )

Python also has a special function called atan2() from NumPy to calculate arctangent using the (x, y) coordinates of a point in the Cartesian plane.

atan2(y, x)

The variables x and y represent the coordinates of a point on the two-dimensional Cartesian plane (x, y).

The atan2() function calculates the arctangent of the arc determined by the point (x, y) on the plane.

Note. Unlike the arctan() function, the atan2() function measures the continuous arc length even beyond the angle of π/2.

Examples

Example 1

Given a tangent of tan(θ) = 3.73, find the angle θ of the tangent.

>>> from numpy import arctan
>>> x=3.73
>>> arctan(x)

The result of the arctan() function is the arctangent, which measures the arc on the circumference identified by the tangent.

1.3088594904685142

In this case, the result is 1.3088594904685142, which is the angle θ of the tangent in radians.

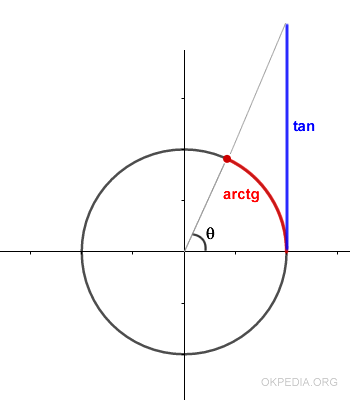
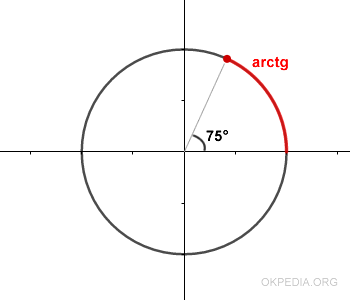
The angle θ of the tangent measures 1.3 radians (approximately 75.1°).

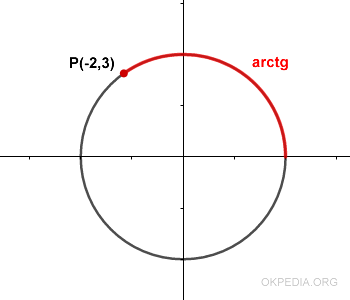
Example 2

Given a point P(-2, 3) on the plane, find the arctangent.

>>> from math import atan2
>>> atan2(3,-2)

The output of the atan2() function is 2.158798930342464, which measures the arc described by point P in radians.

2.158798930342464

The arc described by point P measures 2.15 radians.

Note. In the function atan2(y, x), the coordinates are inverted with respect to mathematical notation (y, x). Therefore, the point (-2, 3) is denoted as atan2(3, -2).