Cosa sono gli integrali
In matematica esistono due tipi di integrali (definiti e indefiniti) che hanno scopi differenti:
- Gli integrali definiti permettono di calcolare l'area di una superficie regolare o irregolare. Nel simbolo dell'integrale sono indicati gli estremi a,b di integrazione. Il risultato è un numero reale. $$ \int_a^b f(x) \: dx \: = r $$
- Gli integrali indefiniti calcolano la primitiva di una funzione. Sono l'operazione inversa della derivata. Per questo sono anche detti antiderivata. Nel simbolo non sono indicati gli estremi di integrazione. Il risultato è una famiglia di funzioni primitive. $$ \int f(x) \: dx \: = F(x)+c $$
In entrambi i casi la funzione all'interno dell'integrale è detta funzione integranda. Il simbolo "dx" è invece detto differenziale della variabile di integrazione.
Qual è la differenza tra integrale definito e indefinito
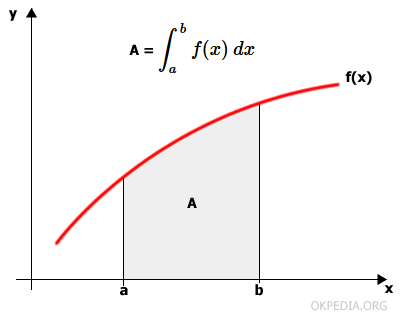
L'integrale definito misura l'area (A) della funzione tra il grafico della funzione f(x) e l'ascisse (x) in un intervallo (a,b). Quindi, è un numero reale.
L'integrale indefinito calcola l'antiderivata (o primitiva) di una funzione. Quindi, è una famiglia di funzioni del tipo F(x)+c.

Cos'è una primitiva? Una funzione F(x) si dice primitiva di un'altra funzione f(x), se la derivata di F'(x) è uguale a f(x). Ogni funzione ha infinite primitive perché la derivata di qualsiasi costante (c) è sempre nulla.
Come calcolare gli integrali?
L'integrale indefinito è l'operazione inversa della derivata.
Esempio. $$ \int 2x \: dx = x^2 + c $$
Pur avendo scopi diversi, il calcolo di un integrale definito può essere svolto tramite le regole degli integrali indefiniti con il teorema fondamentale dell'integrazione
$$ \int_a^b f(x) \: dx \: = [F(x)]_a^b = F(b) - F(a) $$
Si può usare soltanto se le funzioni sono continue e derivabili.
Esempio. $$ \int_3^5 2x \: dx = [x^2]_3^5 = 5^2 - 3^2 $$
