How to calculate indefinite integral in python

To calculate the indefinite integral of a function ( antiderivative ) in python, we use the integrate() of sympy.

integrate(f,x)

• The first argument f is the integrand function.
• The second argument x is the integration variable (dx). The variable must be defined as a symbol.

The output is the primitive function F(x).

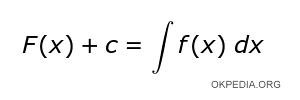
Note. It is the inverse operation of the derivation. For this reason, the indefinite integration is also called antiderivative.

Examples

Example 1

This script calculates the indefinite integral of f(x)=2x.

import sympy as sp
x = sp.Symbol('x')
sp.integrate(2*x, x)

The first statement loads the sympy library.

The second statement defines the variable x as a symbol by the function Symbol().

The third statement calculates the integral of the function 2 * x by integrate().

The output is

x**2

The primitive function of 2x is x².

$$ \int 2x \; dx = x^2 +c $$

Example 2

This script calculates the primitive function of sin (x)

import sympy as sp
y=sp.sin(x)
sp.integrate(y, x)

The output of the function is

-cos(x)

The primitive function of sin (x) is -cos (x).

$$ \int sin x \; dx = -cos x +c $$

Example 3

This script calculates the indefinite integral of x / 5

import sympy as sp
y=x/5
sp.integrate(y, x)

The result is

x**2/10

The primitive function of x / 5 is x² / 10.

$$ \int \frac{x}{5} \; dx = \frac{x^2}{10} +c $$