How to calculate the definite integral in python

To compute the integral defined in python, we use the integrate() function of the sympy library

integrate(y,(x,a,b))

• The first argument y is the integrand function f(x).
• The second argument is the integration variable dx and the integration interval (a, b).

This instruction calculates the definite integral of the function f(x).

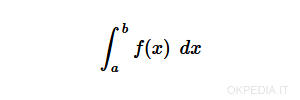
Note. The integration variable (x) must be defined as a symbol. The output of the function is also returned in symbolic form.

Examples

Example 1

This script calculates the definite integral of f(x) = 3x in the interval (5,7)

import sympy as sp
x = sp.Symbol('x')
y=3*x
sp.integrate(y,(x,5,7))

The output is

36

The definite integral of 3x in the interval (5,7) is 36.

$$ \int_{5}^{7} 3x \:\: dx = 36 $$

Example 2

This script calculates the definite integral of f(x) = 5x in the interval (1,3)

import sympy as sp
x = sp.Symbol('x')
y=5*x
sp.integrate(y,(x,1,3))

The output of the function is

20

The definite integral of 5x in the interval (1,3) is 20.

$$ \int_{1}^{3} 5x \:\: dx = 20 $$

Example 3

This script performs the same previous calculation using integrate() as a method

import sympy as sp
x = sp.Symbol('x')
y=5*x
y.integrate((x,1,3))

The result is the following

20

It is the same result as in the previous exercise, the definite integral of 5x in the interval (1,3). However, it is achieved by the method rather than the function.