Comment calculer l'intégrale définie en python

Pour calculer l'intégrale définie en python, nous utilisons la fonction integrate() du module sympy.

integrate(y,(x,a,b))

• Le premier argument y est l’intégrande f (x), c'est-à-dire la fonction à intégrer.
• Le deuxième argument est la variable d'intégration dx et l'intervalle d'intégration (a, b).

La fonction integrate() calcule l'intégrale définie de la fonction f(x).

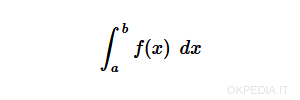
Note. La variable d'intégration (x) doit être définie en tant que symbole. La sortie de la fonction est également renvoyée sous forme symbolique.

Exemples de calcul

Exemple 1

Ce script calcule l'intégrale définie de f (x) = 3x dans l'intervalle (5,7)

import sympy as sp
x = sp.Symbol('x')
y=3*x
sp.integrate(y,(x,5,7))

La sortie de la fonction intégrée () est la suivante

36

L'intégrale définie de 3x dans l'intervalle (5,7) est 36.

$$ \int_{5}^{7} 3x \:\: dx = 36 $$

Exemple 2

Ce script calcule l'intégrale définie de f (x) = 5x dans l'intervalle (1,3)

import sympy as sp
x = sp.Symbol('x')
y=5*x
sp.integrate(y,(x,1,3))

La sortie de la fonction intégrée () est

20

L'intégrale définie de 5x dans l'intervalle (1,3) est 20.

$$ \int_{1}^{3} 5x \:\: dx = 20 $$

Exemple 3

Ce script effectue le même calcul précédent en utilisant comme méthode

import sympy as sp
x = sp.Symbol('x')
y=5*x
y.integrate((x,1,3))

Le résultat est le suivant

20

C'est le même résultat que dans l'exercice précédent, l'intégrale définie de 5x dans l'intervalle (1,3), mais le résultat est obtenu avec la méthode à la place de la fonction.