Comment calculer une intégrale indéfinie en Python

Pour trouver la fonction primitive (intégrale indéfinie) d'une fonction mathématique f (x) en python, nous utilisons la fonction integrate du module sympy.

integrate(f,x)

• Le premier argument f est la fonction integrand.
• Le deuxième argument x est la variable d'intégration (dx). La variable doit être définie en tant que symbole.

La fonction intégrée () renvoie la fonction primitive F (x).

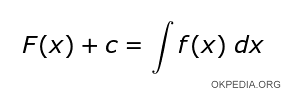
Remarque. La fonction intégrée () effectue l'intégration indéfinie d'une fonction différentiable, c'est-à-dire l'opération inverse de la dérivation. À partir d'une fonction f '(x) en entrée, il calcule la fonction primitive f (x) en sortie.

Exemples

Exemple 1

Ce script calcule l'intégrale indéfinie de la fonction 2x.

import sympy as sp
x = sp.Symbol('x')
sp.integrate(2*x, x)

La première instruction importe le module sympy en python.

La deuxième instruction définit la variable x comme un symbole via la fonction Symbol().

La troisième instruction calcule l'intégrale de la fonction 2 * x avec integrate().

Le résultat en sortie est le suivant

x**2

La fonction primitive de 2x est x².

$$ \int 2x \; dx = x^2 +c $$

Exemple 2

Ce script calcule la fonction primitive de sin(x)

import sympy as sp
y=sp.sin(x)
sp.integrate(y, x)

La fonction renvoie ce résultat à la sortie

-cos(x)

La fonction primitive de sin (x) est -cos (x).

$$ \int sin x \; dx = -cos x +c $$

Exemple 3

Ce script calcule l'intégrale indéfinie de x / 5

import sympy as sp
y=x/5
sp.integrate(y, x)

Le résultat du script est le suivant:

x**2/10

La fonction primitive de x / 5 est x²/10.

$$ \int \frac{x}{5} \; dx = \frac{x^2}{10} +c $$