Come calcolare il rango di una matrice

Per calcolare il rango (o caratteristica) di una matrice, bisogna trovare il minore con determinante diverso da zero di ordine più elevato.

Un esempio di calcolo del rango

Esercizio 1

Data la matrice M con tre righe e quattro colonne (3x4)

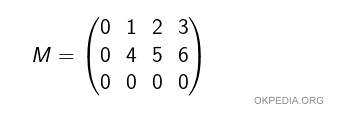
Si calcolano tutti i minori di ordine 1, composti da una riga e una colonna.

E' sufficiente che ci sia almeno un determinante di ordine 1 per affermare che il rango (rk) è uguale o superiore a uno ( rk ≥ 1 ).

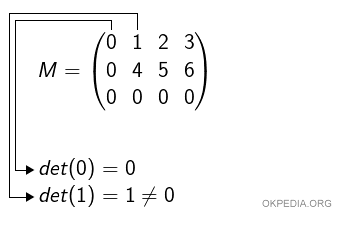
Se esiste, si calcolano tutti i minori di ordine 2, quelli composti da due righe e due colonne.

E' sufficiente che ci sia almeno un determinante non nullo di ordine due per affermare che il rango (rk) della matrice è uguale o superiore a due ( rk ≥ 2 ).

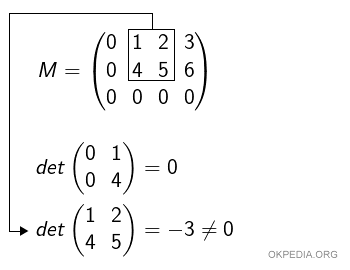
Ora si calcolano tutti i minori di ordine 3, composti da tre righe e da tre colonne.

In questo caso nessun minore ha un determinante diverso da zero.

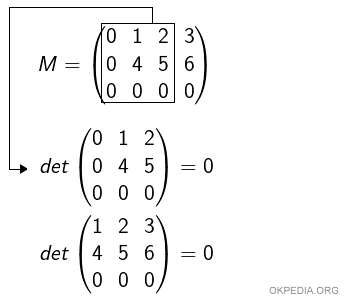
Pertanto, la matrice non ha rango uguale a 3 o superiore ( rk < 3 ).

Nota. Se i minori di ordine N sono nulli, allora sono nulli anche tutti gli altri minori di ordine superiore (N+1, N+2, ecc. ).

Si può quindi affermare che il rango della matrice è due, perché il minore con determinante diverso da zero è di ordine due.

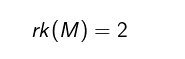
Questo metodo consente di calcolare sia il rango delle matrici quadrate che di quelle rettangolari.