Cos'è il limite di una funzione
Il limite di una funzione f(x) nel punto X0 del suo dominio, se esiste, è il valore a cui la funzione f(x) tende quando l'argomento tende a X0.
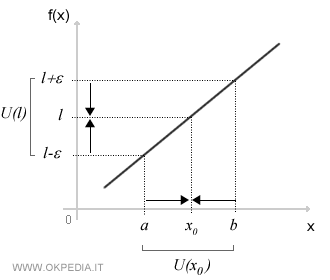
La notazione del limite è la seguente:
$$ \lim_{x \rightarrow x_0 } f(x) = L $$
Si legge "il limite di f(x) se x tende a x0 è L".
- Il punto x0 è detto punto di accumulazione.
- La variabile x è detta argomento del limite.
- Il risultato L è il limite ossia il valore a cui tende la f(x) quando si avvicina a x0.
- Il punto di accumulazione x0 del limite di una funzione f(x) può essere:
- un numero (n) definito del dominio di f(x)
- zero
- + infinito ( +∞ )
- - infinito ( -∞ )
Esempi
Esempio 1
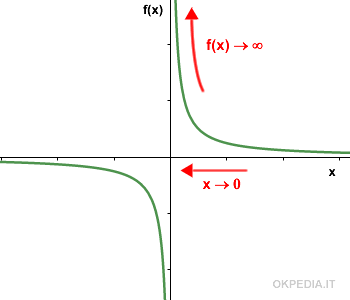
Calcolare il limite della funzione f(x)=1/x per x tendente a zero.
$$ \lim_{x \rightarrow 0} \frac{1}{x} = \frac{1}{0} = +∞ $$
Nel punto x0=0 la funzione non è determinata.
Tuttavia, quando la x si avvicina a x0=0 la funzione f(x) tende a + infinito.
Esempio 2
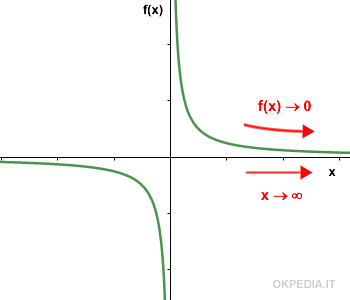
Trovare il limite della funzione f(x)=1/x per x tendente a +∞.
$$ \lim_{x \rightarrow +∞} \frac{1}{x} = \frac{1}{+∞} = 0 $$
Il simbolo +∞ non identifica un punto definito del dominio.
Tuttavia, quando la x si avvicina a x0=+∞ la funzione f(x) tende a zero.