How to calculate the transpose of a matrix in Matlab and Octave

To calculate the transpose of a matrix in Matlab or Octave use the function transpose()

transpose(m)

Alternatively, write the array in this syntax

m'

or in this syntax

m.'

The parameter m is the matrix.

In both cases the transposed matrix of m is generated.

What’s the difference between m' and m.'?

When working with real numbers, there’s no difference between m' and m.'.

However, when dealing with complex numbers:

• m' returns the conjugate transpose - it transposes the matrix (rows become columns) and applies the complex conjugate (flipping the sign of the imaginary part).
• m.' returns the non-conjugate (or simple) transpose - it transposes the matrix without altering the complex values.

Therefore, if you’re working with complex numbers, it’s essential to be aware of this distinction.

What is a transposed matrix? The transpose M^T of a matrix M is the matrix in which the columns of the matrix M are transformed into rows (or vice versa).

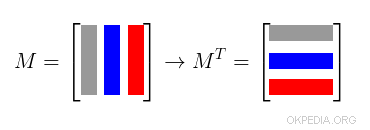
Examples

Example 1

Create a matrix 3x3 matrix

>> A = [1,2,3;4,5,6;7,8,9]
1 2 3
4 5 6
7 8 9

The transpose() function calculates the transpose of matrix A

>> transpose(A)
1 4 7
2 5 8
3 6 9

Example 2

The same result is obtained by writing A'

>> A'

The result is the transposed matrix of A

1 4 7
2 5 8
3 6 9

Example 3

Here’s an example using a matrix of complex numbers:

>> A = [1+2i, 3+4i; 5+6i, 7+8i]

The command A' returns the conjugate transpose - it transposes the matrix (turning rows into columns) and applies the complex conjugate to each element.

>> A'

ans =

1 - 2i 5 - 6i
3 - 4i 7 - 8i

The command A.' - with the dot - returns the non-conjugate (simple) transpose: it transposes the matrix but leaves the complex values unchanged.

>> A.'

ans =

1 + 2i 5 + 6i
3 + 4i 7 + 8i