Cómo calcular la integral definida en python

Para calcular la integral definida en python, se utiliza la función integrate() del módulo sympy

integrate(y,(x,a,b))

• El primer argumento y es el integrando f (x).
• El segundo argumento es la variable de integración dx y el intervalo de integración (a, b).

La función integrate() calcula la integral definida de la función f (x).

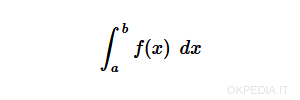
Nota. La variable de integración (x) debe definirse como un símbolo. El resultado también se devuelve en forma simbólica.

Ejemplos de calculo

Ejemplo 1

Este script calcula la integral definida de f (x) = 3x en el intervalo (5,7)

import sympy as sp
x = sp.Symbol('x')
y=3*x
sp.integrate(y,(x,5,7))

El resultado es

36

La integral definida de f(x)=3x en el intervalo (5,7) es 36.

$$ \int_{5}^{7} 3x \:\: dx = 36 $$

Ejemplo 2

Este script calcula la integral definida de f(x) = 5x en el intervalo (1,3)

import sympy as sp
x = sp.Symbol('x')
y=5*x
sp.integrate(y,(x,1,3))

El resultado es

20

La integral definida de 5x en el intervalo (1,3) es 20.

$$ \int_{1}^{3} 5x \:\: dx = 20 $$

Ejemplo 3

Este script realiza el mismo cálculo que el ejemplo anterior utilizando el método integrate

import sympy as sp
x = sp.Symbol('x')
y=5*x
y.integrate((x,1,3))

El resultato es

20

Es el mismo resultado del ejercicio anterior, la integral definida de 5x en el intervalo (1,3), con el método en lugar de la función.