Cómo calcular la integral indefinida en Python

Para calcular la función primitiva (integral indefinida o antiderivada) de una función matemática f (x) en python, usamos la función integrate del módulo sympy.

integrate(f,x)

• El primer argumento f es la función integrand
• El segundo argumento x es la variable de integración (dx). La variable debe definirse como un símbolo.

La función integrate() genera la función primitiva F (x).

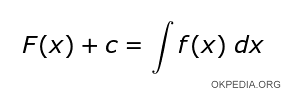
Nota. La función integrada () realiza la integración indefinida de una función. Es la operación inversa de la derivación. Calcula la función primitiva f (x) a partir de una función diferenciable f '(x). Por esta razón, la operación de integración indefinida también se denomina antiderivada.

Ejemplos

Ejemplo 1

Este script calcula la integral indefinida de la función 2x.

import sympy as sp
x = sp.Symbol('x')
sp.integrate(2*x, x)

La primera declaración importa el módulo sympy.

La segunda declaración define la variable x como un símbolo a través de la función Symbol().

La tercera declaración calcula la primitiva de 2*x a través de la función integrate().

El resultado de salida es el siguiente

x**2

La función primitiva de 2x es x².

$$ \int 2x \; dx = x^2 +c $$

Ejemplo 2

Este script calcula la función primitiva de sin (x)

import sympy as sp
y=sp.sin(x)
sp.integrate(y, x)

El resultado de salida es

-cos(x)

La función primitiva de sin (x) es -cos (x).

$$ \int sin x \; dx = -cos x +c $$

Esempio 3

Este script calcula la integral indefinida de x / 5

import sympy as sp
y=x/5
sp.integrate(y, x)

El resultado es el siguiente:

x**2/10

La función primitiva de x / 5 es x² / 10.

$$ \int \frac{x}{5} \; dx = \frac{x^2}{10} +c $$