Calcolare l'integrale definito in python

Per calcolare l'integrale definito in python si utilizza la funzione integrate() della libreria sympy

integrate(y,(x,a,b))

• Il primo argomento y è la funzione integranda f(x).
• Il secondo argomento è la variabile di integrazione dx e l'intervallo di integrazione (a,b).

La funzione integrate() calcola l'integrale definito della funzione f(x).

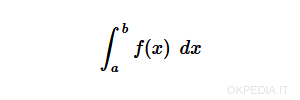
Nota. La variabile di integrazione (x) deve essere definita come simbolo. Anche il risultato in output della funzione è restituito nella forma simbolica.

Esempi di calcolo

Esempio 1

Questo script calcola l'integrale definito di f(x)=3x nell'intervallo (5,7)

import sympy as sp
x = sp.Symbol('x')
y=3*x
sp.integrate(y,(x,5,7))

L'output della funzione integrate() è

36

L'integrale definito di 3x nell'intervallo (5,7) è 36.

$$ \int_{5}^{7} 3x \:\: dx = 36 $$

Esempio 2

Questo script calcola l'integrale definito di f(x)=5x nell'intervallo (1,3)

import sympy as sp
x = sp.Symbol('x')
y=5*x
sp.integrate(y,(x,1,3))

L'output della funzione integrate() è

20

L'integrale definito di 5x nell'intervallo (1,3) è 20.

$$ \int_{1}^{3} 5x \:\: dx = 20 $$

Esempio 3

Questo script compie lo stesso calcolo precedente usando integrate come metodo

import sympy as sp
x = sp.Symbol('x')
y=5*x
y.integrate((x,1,3))

Il risultato è il seguente

20

E' lo stesso risultato dell'esercizio precedente, l'integrale definito di 5x nell'intervallo (1,3) ma ottenuto con il metodo anziché la funzione.