Come calcolare la matrice trasposta in Matlab e Octave
Per calcolare la matrice trasposta in Matlab o Octave utilizzare la funzione transpose()
transpose(m)
In alternativa, scrivere la matrice in questa sintassi
m'
oppure
m.'
Il parametro m è la matrice.
In entrambi i casi viene generata la matrice trasposta di m.
Quale è la differenza tra m' e m.'
Se la matrice contiene numeri reali, non c’è differenza tra m' e m.'.
Tuttavia, se la matrice contiene numeri complessi:
- m' calcola la trasposta coniugata: trasforma righe in colonne e applica il coniugato complesso (cioè cambia il segno della parte immaginaria).
- m.' calcola la trasposta semplice: trasforma righe in colonne, ma lascia invariati i numeri complessi.
Quindi, se si lavora con i numeri complessi è molto importante tenerlo a mente.
Cos'è la matrice trasposta? La matrice trasposta MT è la matrice in cui le colonne sono trasformate in righe (o viceversa).
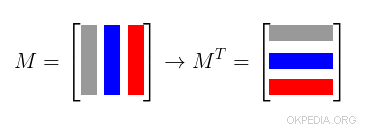
Un esempio pratico
Esempio 1
Creare una matrice
>> A = [1,2,3;4,5,6;7,8,9]
La matrice A è una matrice 3x3
1 2 3
4 5 6
7 8 9
La funzione transpose calcola la matrice trasposta
>> transpose(A)
Il risultato è la matrice trasposta di A
1 4 7
2 5 8
3 6 9
Esempio 2
Lo stesso risultato si ottiene scrivendo A'
>> A'
Il risultato è la matrice trasposta di A
1 4 7
2 5 8
3 6 9
Esempio 3
Facciamo un esempio di matrice con numeri complessi
>> A = [1+2i, 3+4i; 5+6i, 7+8i]
Il comando A' calcola la trasposta coniugata, trasformando le righe in colonne e calcolando il coniugato complesso.
>> A'
ans =
1 - 2i 5 - 6i
3 - 4i 7 - 8i
Il comando A'. con il punto, invece, calcola la trasposta coniugata, trasformando le righe in colonne lasciando invariati i numeri complessi.
>> A.'
ans =
1 + 2i 5 + 6i
3 + 4i 7 + 8i
